volumecubicsample

float  volumecubicsample(<geometry>geometry, int primnum, vector pos)

float  volumecubicsample(<geometry>geometry, string volumename, vector pos)

float  volumecubicsample(<geometry>geometry, int primnum, vector pos, vector &grad)

float  volumecubicsample(<geometry>geometry, string volumename, vector pos, vector &grad)

float  volumecubicsample(<geometry>geometry, int primnum, vector pos, vector &grad, matrix3 &hess)

float  volumecubicsample(<geometry>geometry, string volumename, vector pos, vector &grad, matrix3 &hess)

<geometry>

When running in the context of a node (such as a wrangle SOP), this argument can be an integer representing the input number (starting at 0) to read the geometry from.

Alternatively, the argument can be a string specifying a geometry file (for example, a .bgeo) to read from. When running inside Houdini, this can be an op:/path/to/sop reference.

Returns

The volume primitive’s sampled value at the given position. Values between voxels are evaluated with tri-cubic interpolation.

The grad and hess arguments return the gradient or the hessian of this sampling function which can be computed at the same time as the value.

Returns 0 if primnum or inputnum is out of range, the geometry is invalid, or the given primitive is not a volume or vdb primitive.

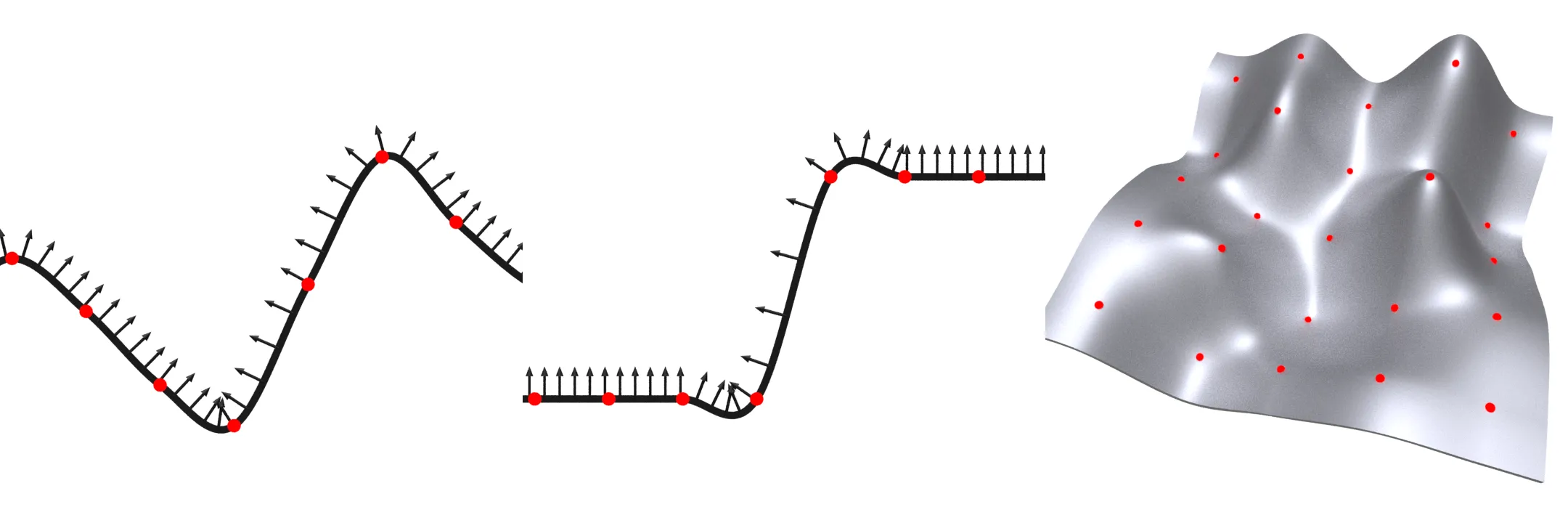Example of interpolation of one and two dimensional data using volumecubicsample. The visualized normal is computed using the grad parameter. Examples

examples

Approximating a volume value at the point P + u using volume values at the point P.

vector  P = {1.0, 2.0, 3.0};
vector grad;
matrix3 hess;
float val1 = volumecubicsample(0, "density", P, grad, hess);

vector u = {0.1, 0.01, 0.001};
float val2 = volumecubicsample(0, "density", P + u);

// By Taylor expansion we have:
// `val1 + dot(u, grad)` is approximately equal to `val2`

// And the second order approximation:
// `val1 + (u, grad) + 0.5 * dot(u, u*hess)`
// is appriximately equal to `val2`